FISIKA TEKNIK ( KESETIMBANGAN MOMEN GAYA )

 

 PENGERTIAN MOMEN GAYA

Besar dan arah efek gaya yang bekerja pda suatu benda tergantung pada  letak garis kerja gaya yang dapat diperinci dengan menentukan jarak tegak lurus antara sebuah titik patokan dengan garis kerja tersebut.

Karena ruang lingkup bahsan adalah benda yang berputar bebas terhadap sumbu dan gaya – gaya sebidang yang bekerja tegak lurus sumbu, maka yang paling penting adalah menetukan titik tersebut yang dinamakan titik pusat koordinat, yaitu titik dimana sumbu memotong bidang gaya yang bekerja.

Jarak tegak lurus antara titik koordinat ke garis kerja gaya dinamakan lengan gaya atau lengan momen dari gaya itu terhadap sumbu.

Dari kedua pengertian diatas, kita dapat peroleh bahwa momen gaya terhadap suatu sumbu adalah hasil kali antara besarnya gaya dengan lengan momen atau disebut juga gaya putar (Torque). Gambaran tentang pengertian tersebut dapat dijelaskan dengan ilustrasi sebagai berikut:

 

 

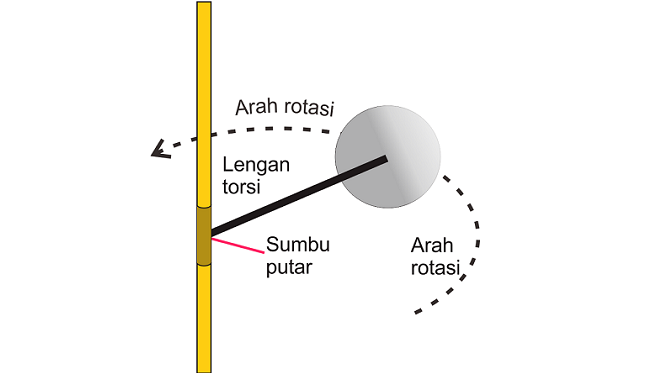
Dari gambar 6.1 b diatas dapat dibedakan bahwa:

Efek gaya F1: rotasi yang berlawanan dengan putaran jarum jam terhadap sumbu dan dianggap positif (+). Sehingga momen G (gamma) dari gaya F1 terhadap sumbu lewat  O:

G₁ = +F₁. l₁

Efek gaya F2: rotasi yang searah putaran jarum jam terhadap sumbu dan dianggap negatif (-).Sehingga momen G (gamma) dari gaya F2 terhadap sumbu lewat  O:

G₂ = -F₂. l₂

Momen ini dapat dinyatakan dalam pound feet atau Kgm.

 

 

 SYARAT KEDUA UNTUK KESETIMBANGAN

Bendayang dalam kondisi setimbang, maka sejumlah gaya yang bekerja padanya harus memenuhi 2 syarat:

1.      Sama besar dan berlawanan arahnya.

2.      Harus mempunyai garis kerja yang sama.

Syarat pertama dapat dipenuhi oleh syarat kesetimbangan I, yaitu:

S Fx = 0,     S Fy = 0

Syarat kedua dapat dipenuhi oleh syarat kesetimbangan II, yang dinyatakan berdasarkan momen gaya, yaitu:

S G = 0 (terhadap sembarang sumbu)

          RESULTAN GAYA SEJAJAR

Resultan gaya sejajar adalah sebuah gaya yang bisa mewakili sekumpulan gaya sejajar serta mempunyai:

Ø  Arah yang sama dengan semua gaya tersebut

Ø  Besar sama dengan penjumlahan besar semua gaya

Ø  Garis kerja yang dapat dicari berdasar syarat bahwa momen resultan harus sama dengan penjumlahan momen setiap gaya.

Gambar 7.3 dapat dipakai untuk menjelaskan hal tersebut. Dari gambar tersebut dengan gaya – gaya sejajar F1 dan F2 dapat dibuat sumbu x yang tegak lurus terhadap gaya – gaya dan titik O adlah titik sembarang yang dijadikan acuan. Karena kedua gaya tidak berkomponen x maka besarnya resultan gaya:

R = S F_y = F₁ + F₂

Sedangkan resultan momennya terhadap titik O adalah:

S G ₀ = x₁ F_­1 + x₂ F₂

Dan jika  adalah jarak dari O ke garis kerja resultan, maka momen dari resultan terhadap O adalah:

R  = (F₁ + F₂)

Biasanya  dapat ditentukan dengan:

S G ₀ = R

x₁ F_­1 + x₂ F₂ = (F₁ + F₂)

Resultan dari sembarang gaya sejajar dapat ditentukan dengan cara yang sama degan besar resultannya:

R = S F

Dan jika gaya – gaya itu sejajar dengan sumbu y, maka koordinat x dari garis kerjanya (resultan) adalah:

  PUSAT BERAT

Berat adlah resultan dari semua gaya tarik bumi yang dialami oleh partikel zat dalam suatu benda. Tetapi karena jarak ke pusat bumi sedemikian jauhnya sehingga gaya – gaya tersebut dapat dianggap sejajar. Dengan demikian berat benda dapat diartikan sebagai resultan dari sejumlah besar gaya sejajar.

Sedangkan pusat berat dari benda dapat diilustrasikan dari gambar berikut yang memperlihatkan benda tipis sembarang bentuk dan terletak pada bidang xy. Jika dimisalkan benda tersebut terbagi atas partikel – partikel dengan berat w1, w2 dst maka:

 

 

Berat total benda tersebut adalah:

W = w1 + w2 + ... = S w

Koordinat x garis kerja W adalah:

Kemudian jika gaya gravitasi kita putar 90⁰ berlawanan jarum jam, maka koordinat y dari garis kerjanya adalah:

Titik perpotongan garis kerja W pada kedua bagian dengan koordinat , dinamakan pusat berat benda tersebut. Dan simetri suatu benda seringkali berguna untuk menentukan pusat berat benda.

 

 

 

5.5            KOPEL

Kopel adalah pasangan gaya sama besar yang berlawanan arah, denga garis kerja sejajar tetapi tidak berimpit. Pasangan gaya tersebut dapat dijelaskan dengan gambart berikut ini, yang sama besar masing – masing gaya adalah F, terpisah oleh jarak tegak lurus l.

Resultan dari gaya – gaya tersebut adalah:

R = F – F = 0

Dengan resultan = 0 artinya bahwa sebuah kopel tidak mempengaruhi sebuah gerak translasi benda sebagai suatu benda keseluruhan, tetapi hanya menimbulkan rotasi.

Momen resultan dari kopel tersebut terhadap sembarang titik O adalah:

                                                S G ₀    =  x₁F – x₂F

                                                            = x₁F – (x₂ + l) F

                                                            =  - lF

Dari perumusan itu dapat disimpulkan bahwa besarnya momen kopel terhadap semua titik dalam bidang dimana bekerja gaya – gaya yang membentuk kopel adalah:

Hasil kali salah satu gaya  dengan jarak tegak lurus antara garis – garis kerjanya.

Dan sebuah benda yang padanya bekerja sebuah kopel, hanya dapat dalam keadaan setimbang bila ada kopel lain yang bekerja pada benda tersebut dengan besar yang sama dan arah berlawanan.

Contoh Soal:

1.      Sebuah tangga panjang 20 feet, berat 80 lb pusat beratnya ada ditengah – tengah, dalam keadaan setimbang, bersandar pada dinding vertikal tanpa gesekan dan membuat sudut 53⁰ denganhorizontal. Tentukan besar dan arah gaya F1 dan F2.

 

 

 

 

Penyelesaian:

Bila tanpa gesekan, F1 horizontal dan arah F2 tidak diketahui, sehinga F2 diuraikan menjadi F2x dan F2y.

Syarat I kesetimbangan, memberikan persamaan:

                                S Fx       = F₂ cos q  - F₁  = 0

                                S Fy       = F₂ sin q  - 80  = 0

                                                        F₂ sin q    = 80 lb

Syarat kesetimbangan II, momen terhadap sumbu lewat titik A

                                S G _A      = F₁  x 16  - 80 x 6   = 0

                                                                        F₁  = 480/16

                                                                        F₁  = 30 lb

Dimasukkan ke persamaan 1 sehingga: F₂ cos q = 30 lb

Karenanya:

                                        F₂  =

                                              = 85,5 lb

q        = tan ^-1 (80:30)

= 69,5⁰

2.      Tentukan letak pusat berat bagian suatu mesin sperti gambar. Yanbg terdiri atas piringan berdiameter 2 inci dan panjangnya 1 inci dan batang berdiameter 1 inci serta panjangnya 6 inci. Keduanya terbuat dari bahan homogen.

 

 

 

Penyelesaian:

Berdasar simetri  pusat berat berada pada sumbu sumetrinya, sedagkan pusat berat masing – masing terletak pada tengah – tengah antara ujungnya masing – masing.

Volume piringan:

                                    Voll    = p R² x 1

                                              = p  . (1)² x 1

                                              = p in³

Volume batang:

                                    Voll    = p R² x 6

                                              = p  . (0,5)² x 6

                                              = 3p / 2 in³

Karena berat kedua bagian berbandinga langsung dengan volumenya, maka:

Ambillah titik O pada muka sebelah kiri dan pada sumbu piringan, maka:

x₁ = 0,5 in dan x₂ = 4,0 in

   sebelah kanan O

 

3.      Pada soal 1 dapat dianggap dipengaruhi oleh 2 buah kopel,

a)      Dibentuk oleh gaya F2 sin q

G ₁ = 6  ft x 80 lb = 480 lb       searah jarum jam

b)      Dibentuk oleh F2 cos q dan F1

G ₂ = 16  ft x 30 lb = 480 lb     berlawanan jarum jam